Soil particles in a soil mass experience weight of everything above them which includes weight of all the soil particles above them, weight of water and weight of structure if present, and because of that they experience stress in between the soil particles which we call total stress.

But if we put this soil mass in water then because of buoyancy force the net total downward force is reduced consequently the stress on particles is reduced. This reduced stress is called effective stress.

The stress exerted by the water present in the soil pores is called the pore water pressure.

We can write expression for effective stress as this

Effective stress is different at different depths below ground surface because total stress and pore water pressure changes at different depth.

We know that stress at any point or plane under the soil can be given as force on that plane divided by the area of the plane.

Force on that plane is the weight of soil above the plane and that is unit weight of soil multiplied by its volume. Volume is area multiplied by the height of the soil mass.

This can be simplified to this:

σ = γH

So we can directly write the stress under any material as unit weight of the material multiplied by the height of the material above that point.

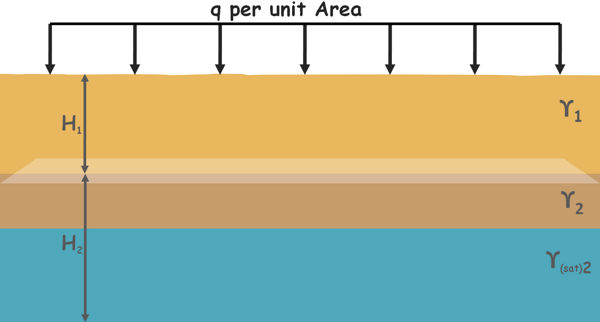
We will consider a case where a soil mass, which consists of two soil deposits of bulk unit weight γ₁ and γ₂, of thickness H₁ and H₂ respectively, is subjected to a surcharge.

Surcharge is the additional load on the soil which may be created due to any overlying structure or any moving object.

Let us assume that soil is subjected to a surcharge of intensity q per unit area. Water table lies somewhere inside the bottom soil deposit. Because of the water table soil becomes completely saturated and unit weight of soil becomes γ_(sat)2.

We will try to determine the effective stress at different depths.

Notice that surcharge load is given as force per unit area, which is equivalent to pressure or stress. So it can be directly used in the equations to provide stress at any depth.

Let’s begin with the soil surface. Total stress on the surface of the soil is because of the surcharge only. So total stress is equal to the surcharge q.

σ = q

No water present above this plane, hence pore water pressure is zero.

u = 0

So effective stress which is total stress minus pore water pressure is q.

σ’ = σ – u

σ’ = q – 0

σ’ = q

Now move a little downward and calculate effective stress at the plane where the two soils meet each other.

We can also take this plane anywhere in the top soil layer but result will be similar and only the depth of the observation will change.

Total stress at this plane is surcharge load q plus stress due to weight of the soil layer above γ₁H₁.

σ = q + γ₁H₁

No water is present above this plane so pore water pressure is zero.

u = 0

so effective stress is equal to the total stress.

σ’ = σ – u

σ’ = σ = q + γ₁H₁

Now let us calculate the effective stress on the plane at the bottom of the bottom soil deposit.

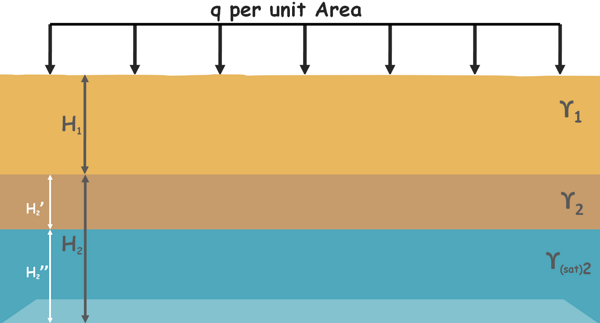
Total stress at this plane is surcharge stress q plus stress because of top not saturated soil layer γ₁H₁ plus stress because of the unsaturated part of the lower soil deposit of thickness say H₂’,γ₂H₂’ plus stress due to saturated soil of thickness say H₂’’γ_(sat)2H₂''.

σ = q + γ₁H₁ + γ₂H₂’ + γ_(sat)2H₂''

Pore water pressure at this plane is because of this water present above it

u = γ_wH₂''

Hence effective stress is total stress minus pore water pressure.

σ’ = σ – u

σ’ = (q + γ₁H₁ + γ₂H₂’ + γ_(sat)2H₂'') – (γ_wH₂'')

σ’ = q + γ₁H₁ + γ₂H₂’ + (γ_(sat)2 – γ_w)H₂''

we can write this quantity as submerged unit weight of soil

σ’ = q + γ₁H₁ + γ₂H₂’ + γ₂‘H₂''

We can notice in all our calculations for effective stress at different depths because of the surcharge load effective stress increased by the surcharge load q at all the depths.