A Soil mass is the huge collection of small particles we call soil grains. These soil grains have mass so they exert force as weight downwards on other particles. Weight is a force and we represent it in Newton or Kilo Newton.

These soil grains due to their own weight gets pushed by all the surrounding particles and exert force on each other which is represented by a quantity we call Stress.

Stress is defined as the force divided by the area over which it applies.

It expresses the internal forces that particles of a material exert on each other.

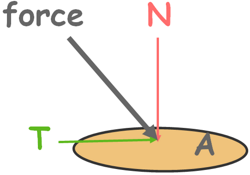
The stress is a vector quantity just like the force. So we can decompose it into normal stress (σ) and shear stress (τ).

The stress developed on a surface because of the force component perpendicular to its area is called normal stress. N is the force component normal to the surface of area A

And the stress developed in the surface because of the force component tangential to its area is called shear stress.

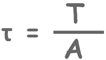
When a soil mass is subjected to an external load, such as load due to overlying structure, the state of stress within the soil changes and that may affect the stability of the soil mass and deformations may occur to the surrounding soil. So it is necessary to analyse the stresses within the soil mass.

Total stress on an element in the soil is equal to the force on that element divided by the area of that element over which the force is acting. Force on that element is the weight of everything above that element which includes soil’s own weight and weight of overlying structure if present. We can understand this stress as the pressure of the overburden.

This total stress in the soil is shared by the two components of the soil mass.

Part of the stress is shared by soil grains that are in contact with each other by their grain to grain force transfer, which is called the effective stress.

And part of the stress is shared by the other component water present in the voids of the soil structure. This is called pore water pressure.

Let us consider a soil mass which is fully saturated. Imagine this soil experiences the force P at some point in soil because of its own weight. This force is resisted partly by the inter-particle forces at the point of contact and partly by the force exerted by water available in pores that is pore water pressure force.

Now take an imaginary plane XX at any level in the soil mass which passes through all the points of contact between soil particles that lie in this plane. This plane may look wavy on the small scale, as it will pass through only the contact areas of the soil particles, but for all practical purposes on the mass scale we can consider it perfectly plane. We will try to analyse the forces on this plane.

The total normal stress on this plane can be given as total normal force acting on the plane divided by area of the plane let’s say capital A.

The inter-particle forces are random in magnitude and direction throughout the soil mass, so on this plane XX at every point of contact we can resolve them into normal and tangential components.

Let’s say the normal component of the force acting on a particle is capital N. so sum of all these normal forces is ΣN.

ΣN = N₁ + N₂ + N₃ + ........

The water filled in the voids of the soil also exerts pressure on soil grains in all directions as the Pascal’s law suggests. This exerted pressure by the pore water is called the pore water pressure. This pressure exerted by water also supports the stress due the weight of overlying material.

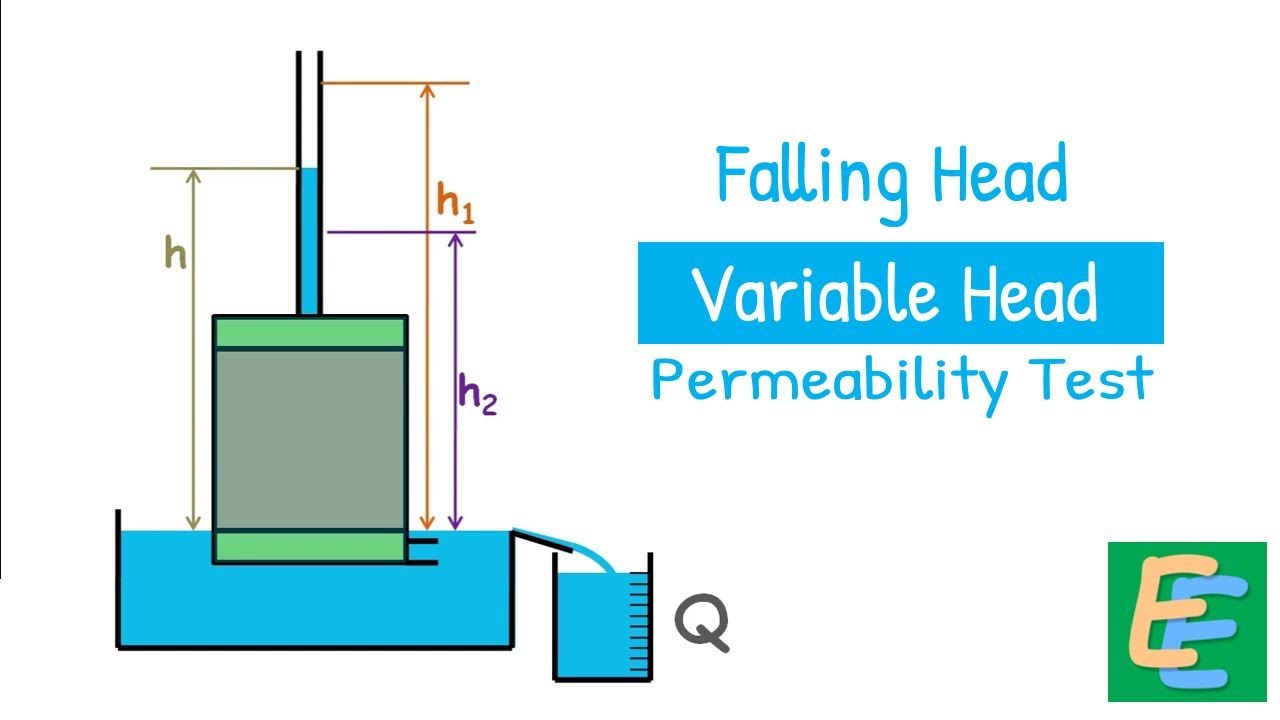
This pore water pressure can be easily measured by inserting a standpipe or tube inside the soil at the location where we want to measure the pressure.

Let’s say the pore water pressure is u at the plane. So the total force offered by pore water pressure force is u multiplied by the area of voids in which water is present in this plane. We say that area as A_w.

U = u.A_w

Let’s say the sum of all pore water pressure forces is ΣU.

ΣU = U₁ = U₂ + U₃ + ..........

Now by applying equation of equilibrium on the plane XX we can write the total normal force acting on this plane is equal to the sum of all normal inter-particle force and pore water pressure force.

Divide the equation by whole cross-sectional area A of the plane.

We can write pore water pressure force as this:

If we notice the area of contact of soil particles, let’s say A_s, is very very small and almost all the area of this plane is covered by the voids A_w.

So, in our equation, area of voids A_w and total area of the plane A can be considered almost equal.

and the value (P/A), we have already noted, is the total normal stress σ on the area. So we get this.

In this equation highlighted quantity is called the effective stress. It is generally denoted by sigma prime (σ') or sigma bar. We can say that effective stress is the pressure transmitted through particles’ contact with each other.

It must be noted that effective stress is equal to the total normal force transmitted at the points of contact divided by the total area of the plane which includes the area of the voids that are occupied by the water as well. This effective stress is much smaller than the actual contact stress which will be the total normal force that is transmitted at the points of contact divided by the actual contact area only.

This quantity will be huge.

So the effective stress has no physical meaning and therefore it cannot be measured directly. But it is deducted from two physical and measurable quantities total stress and pore water pressure.

But still effective stress is very important and useful for soil engineers. It has been observed experimentally that it is the effective stress that determines the engineering behaviour of the soil like compression and shear strength, not the total stress.

We know total stress at any point within a soil mass can be written as this:

total stress(σ) = effective stress(σ’) + pore water pressure(u)

σ = σ' + u

from this we can write expression for effective stress:

σ’ = σ – u

This relationship was proposed by Terzaghi in 1936.

As both the total stress and pore water pressure can actually be measured in the field, we can also calculate the effective stress.

Let us consider a soil mass and try to find out the effective stress at some point below ground at depth capital H.

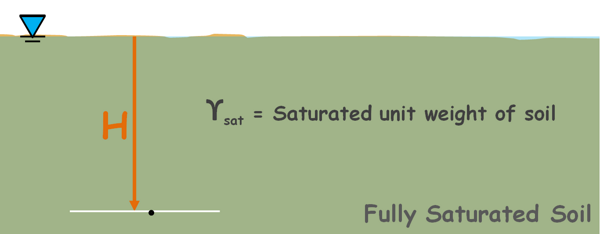
For simplicity we assume that the water table is at the ground level and the soil is completely saturated. Let the saturated unit weight of the soil is γ_sat.

We know unit weight of soil is the weight of the soil divided by its volume.

Total stress at any point is equal to the weight of everything above that point including soil, water and overlying structure if any divided by the area over which this weight is acting.

It can be imagined similar to the pressure which is the force by area.

Here let’s say area over which this weight is acting is capital A.

So weight of the soil above the point of interest will be unit weight of the soil multiplied by the volume of the soil which is its area multiplied by its height.

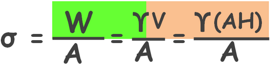
It can be simplified to this.

σ = γH

In our case we have taken unit weight of the soil as saturated unit weight.

σ = y_satH

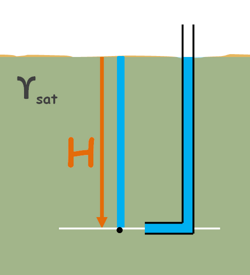
Now the pore water pressure at this point in the soil is the pressure due to the weight of water column above it of height H. So pore water pressure at this point is also the weight of water column divided by the area. So pore water pressure can be written, similar to the total normal stress, as this.

u = y_wH

Here y_w is unit weight of water. We will find this pore water pressure similar if we insert a tube or a standpipe at this point in the soil and observe the rise of water because water in the soil is also at atmospheric pressure and water level will be the piezometric level.

Therefore, the effective stress at this point in the soil can be given as this.

σ' = σ − u

= y_satH - γ_wH

The increase in the effective stress causes the particles to pack more closely which results in decrease in the void ratio because of decrease in volume of voids and that leads to a decrease in compressibility and increase the shearing resistance of the soil.

In the calculation of effective stress we assume that the soil is isotropic that means the unit weight of the soil is constant throughout the soil layer.

But in the actual field conditions soil structure is non homogeneous and not isotropic and contains various defects.