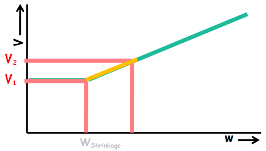
With the increase in the water content of the soil its volume remains constant till all its pores fill completely with water and reaches to its shrinkage limit. When the water content of the soil is further increased beyond the shrinkage limit, soil’s volume also begins to increase.

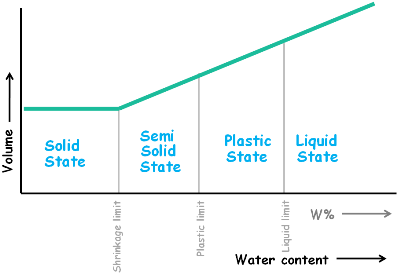
Let’s look at this graph of the soil’s volume change with its water content change. We can see that volume of the soil is constant with the increase in the water content till its shrinkage limit and after that with increase in water content its volume increases.

Here we define a quantity called Shrinkage ratio as an indicator of how much volume change is possible as changes in water content above the shrinkage limit occur.

We indicate Shrinkage Ratio as SR and it is defined as the ratio of the volume change of the soil above shrinkage limit, which we express in the percentage of the soil’s minimum volume that is when it was at shrinkage limit, to the corresponding change in water content.

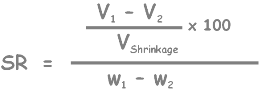
We define shrinkage ratio for volume change above shrinkage limit, simply because below shrinkage limit no volume change occurs in the soil. Volume of the soil remains constant and for any two water content values their corresponding volumes V₁ and V₂ will be equal. Hence the Shrinkage ratio will be zero.

Here this is the minimum volume of the soil which is equal to the volume of the oven dried soil and that may be written as V_Dry.

We can also look at Shrinkage Ratio this way:

If we change water content of a soil by one unit then its percent volume change by its completely dry volume is SR.

We may also say Shrinkage ratio is the rate of percent change of soil volume by its dry volume with respect to water content of the soil.

Now let’s discuss a particular case for the shrinkage ratio.

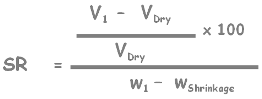
When the volume of the soil reduces to or increases from shrinkage limit then either V₁ or V₂ will become V_Dry and corresponding w₁ or w₂ will become w_Shrinkage that is water content of the soil at shrinkage limit.

It doesn’t matter soil’s volume increases from shrinkage limit or reduced to shrinkage limit, shrinkage ratio will be same. Only the values in the equation will be interchanged.

Here we write volume of soil at shrinkage limit as V_Dry and water content as w_Shrinkage.

Now let’s draw the block diagram of the soil mass when it is at the shrinkage limit. Soil has only two constituents and that are water and solids. If we increase the water content of the sample, weight and volume of the solids is going to remain the same and only weight and volume of the water will increase.

Hence the volume increment of soil is actually the increase in volume of water.

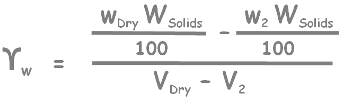
From this we can write the unit weight of this water gamma w as this.

Here we can write these weights of water as water content of the soil at shrinkage limit and at another state.

We know water content is defined as the weight of water divided by weight of solids, and we multiply it by 100 to represent it in percentage.

So it will become this.

Simplify it a little

and write it in this form

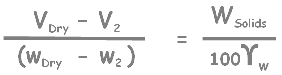
Now this is our Shrinkage Ratio equation

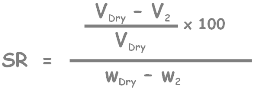
rewrite it by simplifying as this.

We can see we have just calculated this quantity (highlighted), so substitute that here.

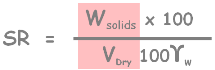
Now we know this quantity (highlighted) is actually dry unit weight of soil. Finally we get this relationship.

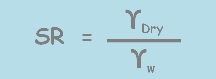
This says in our particular case that when the volume of the soil reduces to or increases from shrinkage limit then that soil’s shrinkage ratio will be equal to ratio of dry unit weight of the soil to the unit weight of the water.

Note that if all the measurements are in gram per cc then unit weight of water will become 1 and Shrinkage Ratio will become equal to the unit weight of dry soil.